CADTOOLフレーム構造解析、FAQ方式の基礎知識集

使用する材質毎に各応力に対する基準強さ（以下、許容応力度を含む）が設定されており、その基準強さを応力で割ったものが安全率となります。

安全率をどのように判断するかは基準強さの設定内容によりますので次で説明します。 なお安全率の表示が"*****" とアスタリスクで表示されている場合は安全率が１００万以上のときに表示されるもので応力がほぼゼロなので強度的には問題がない場所になります。

使用する材質毎に各応力に対する基準強さ（以下、許容応力度を含む）が設定されており、その基準強さを応力で割ったものが安全率となります。

安全率をどのように判断するかは基準強さの設定内容によりますので次で説明します。 なお安全率の表示が"*****" とアスタリスクで表示されている場合は安全率が１００万以上のときに表示されるもので応力がほぼゼロなので強度的には問題がない場所になります。

座屈とは断面に比して長さの大きい部材が圧縮を受けたときに圧縮によるよりも曲げによって破壊される現象のことで、座屈が発生する座屈荷重を圧縮荷重で割ったものが座屈安全率となります。

座屈荷重は断面の最小断面２次半径と部材の長さより公式で求められ、計算結果に表示される座屈荷重は両端支持でオイラーの公式かランキンの公式で適用範囲内のものが使用されます。 また断面選択ダイアログにある座屈チェック機能は独立した計算機能で長さを入力すると選択した断面の各種公式による座屈荷重を求めることができます。

座屈荷重は前述のように公式から求められますが実際に座屈する荷重は部材の取り付けや荷重の掛かり方などで公式の計算値より低下することも考えられますので、 座屈安全率は１以上で安全と判断するのでなく前述のような影響を総合的に判断して余裕を見ておく必要があります。 なお柱の途中に節点があると座屈荷重を計算する部材長さが短くなり座屈荷重が大きくなってしまいます。必要に応じて節点を削除するか座屈チェック機能で別途計算してください。

また応力の安全率と同様に表示が"*****" とアスタリスクで表示されている場合は座屈安全率が１００万以上のときか軸力が引張りの場合に表示されるもので座屈する可能性がほぼゼロの部材になります。

任意の断面で「横座屈」を求める計算式が見つかっておりませんのでフレーム構造解析では「横座屈」は考慮されておりません。

「横座屈」に対する強度の検討が必要な場合は手計算等で求めることが必要となりますが手計算の方法等については提供しておりません。

相当曲げモーメントと相当ねじりモーメントは主に機械設計で軸の強度計算を行うときに用いるもので曲げとねじりが同時にかかったときにどちらか一方にまとめて強度を評価するものになります。 したがって断面形状も円が基本となっています。

出所は前出の「ＪＩＳにもとづく機械設計製図便覧 第１０版（理工学社）」など機械設計の参考書に出ていますが曲げモーメントをＭ、ねじりモーメントをＴとすると次の式で求められます。

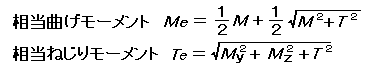
これを形鋼のような断面形状に適用すると過大な値が出るので丸棒や鋼管等で構成する構造に限って使うのが良いと考えられます。 ただしフレーム構造解析は機械設計も含めた汎用の解析ソフトなので設計者が不要なら評価対象として使わない、出力もしないというスタンスで計算結果には表示するようになっています。

なお次で説明する合成応力にも相当曲げモーメントや相当ねじりモーメントから算出された相当曲げ応力や相当ねじり応力が使うことができますが形鋼等の断面形状では合成応力も過大な値が出てしまうことがあります。 合成応力の算出にこれらの応力を使わない、相当曲げ関係・相当ねじり関係の計算結果を出力しないようにする設定はプルダウンメニューの環境設定から計算条件・単位設定ダイアログにある合成応力算出方法をチェックします。 前述のように断面形状が円以外の場合はこれをチェックしておいた方が良いでしょう。

合成引張り応力は断面形状を正方形と仮定して部材Ｙ軸と部材Ｚ軸の曲げモーメントによる引張り応力が一方の角で重なるので、 まずその二つを合成（単純加算）し、更に軸力が全体に働くとして軸力による引張り応力を合成（これも単純加算）したものです。
合成圧縮応力も同じ考え方で各軸の曲げ応力による圧縮応力を合成しそれに軸力による圧縮応力を加算して求めています。
合成せん断応力は部材Ｙ軸と部材Ｚ軸のせん断応力を自乗して足したものの平方根をとって合成し、さらにねじりモーメントによるせん断応力を加算しています。 以上の考え方をまとめたものが次の式になります。

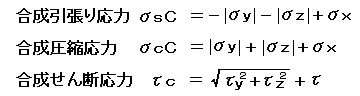
これらの合成応力の計算式は文献等にはっきり明記されているものが見つかりませんでしたので独自に考えたものになります。 なおＡ５で説明したように合成応力に使う曲げモーメントやねじりモーメントに相当曲げモーメント、相当ねじりモーメントを使うかどうかは合成応力算出方法の設定によります。

合成応力の計算式についてはＡ６（詳しくはマニュアルを参照）で説明していますが、合成応力は各軸の応力を合成していますので合成しない単独の応力値に比べて当然高い応力値が出ます。

従来、強度判定を各軸単独の応力値で評価されていたのであればそちらで強度判定を行い、合成応力での判断は必要ありません。 ただし設計者にはより多くの情報が提供された方が良いと考えて計算結果に加えています。評価の参考になりそうであれば使ってみる程度のものとお考えください。

また前述のように合成応力の算出に相当曲げ応力・相当ねじり応力を使うと過大な合成応力値（安全率は過小）となる場合がありますので必要に応じて合成応力算出方法の設定を変更してください。 さらに合成応力を含む計算結果をそのままを客先に見せてしまうと安全率が小さくてビックリされる例も聞いております。 その場合は出力テンプレートの設定により合成応力を出力しないようにもできますので必要に応じて出力テンプレートを設定してください。

節点の座標値や変位などは全体座標（方向や記号が不変）を使いますが、部材（構造要素）は３次元の自由な方向に配置ができ、 断面を回転させることも可能ですので断面性能や部材毎の計算結果を全体座標で扱うことはできません。
そこで部材毎に座標を決めて断面性能や計算結果を扱うようにしています。その部材毎の座標系を部材座標といいます。 ここで全体座標と部材座標、部材回転角の関係を確認しておきましょう。

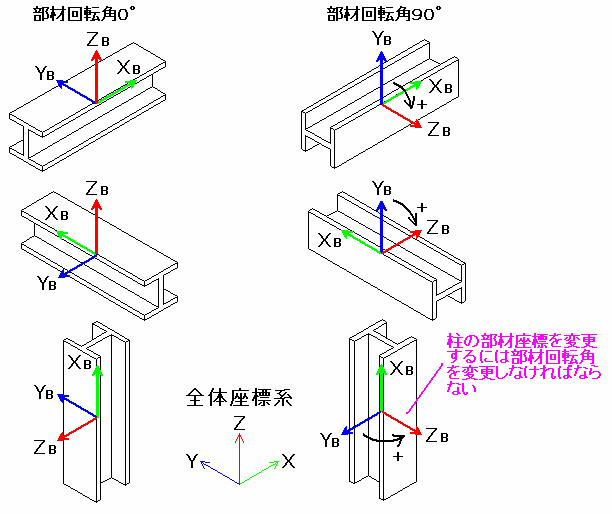
部材座標は部材の軸方向をＸ軸として、そのＸ軸が水平になるように部材を配置したときの断面（回転角は０）の上方向がＺ軸、水平方向をＹ軸としています。 また部材座標に関係した計算結果には“Ｂ”が付くようになっています。
例えば部材Ｙ軸周りの曲げモーメントはＭｙＢになり、部材Ｚ軸方向のせん断力はＦｚＢになります。 ここで断面２次モーメントや曲げモーメント、曲げ応力は部材座標の軸周りで扱い、せん断力やせん断応力は部材座標の軸方向となっています。 特にモーメント関係の軸周りの考え方は変形の方向とは９０度異なる方向になりますので注意が必要です。

部材座標は３次元の構造解析をする上で重要ですのでマニュアルやチュートリアルを参照して十分に理解しておいてください。 またイメージ表示条件設定で部材座標をイメージ表示する機能もありますので慣れるまでは部材座標を表示させて確認してみると良いでしょう。 イメージ表示条件設定で部材座標を表示した場合に緑線が部材座標のＸ軸、赤線がＺ軸、青線がＹ軸を示します。

フレーム構造解析では部材座標で断面２次モーメントの大きい方の軸を強軸とし、小さい方を弱軸としています。
問い合わせの中で「従来は曲がりにくい方向を強軸と呼んでいた」という方がおりましたが、 断面２次モーメントも部材座標の軸周りで扱うので曲がりにくい方向とは９０度異なる軸が強軸となりますので逆ではないかと思われたようです。

イメージ表示条件設定では部材座標のイメージの強軸のみ太く表示させることもできます。 ここで強軸、弱軸は前述のように断面２次モーメントで判断しますが断面２次モーメントは軸周りという扱いになっていますので、 例えば横に長く縦に薄い平鋼を考えた場合、断面２次モーメントは部材座標のＺ軸（上方向）が大きいのでＺ軸の赤線が太くなりますが、 断面が縦に長いものは部材座標のＹ軸（水平方向）周りの断面２次モーメントが大きくなりますので部材座標のＹ軸の青線が太くなります。 部材座標は強軸、弱軸で色分けてしているわけではないので注意してください。

業界や会社によってはこの考え方と異なる場合もあるかも知れませんがフレーム構造解析では上記の考えになっているということをご理解ください。

フレーム構造解析のモーメントの正負は機械学会の取り決めにしたがっていて、例えば両端支持はりで上から荷重がかかって下にたわんでいる状態のモーメントを正とします。建築系とは逆の取り決めのようです。
また前述のようにモーメントは部材座標系の軸周りの値になっていますのでこれも注意が必要です。

モーメントの値をモーメント線図にするときには例えば部材Ｙ軸周りのモーメントは部材座標のＸ－Ｚ平面に作図するのですがこの時はＺ軸方向を正としてモーメント線図を作図しています。 部材Ｚ軸周りのモーメントは部材Ｘ－Ｙ平面でＹ軸方向を正として作図します。

以上の仕様でモーメント線図を作図しているのですが正の方向の取り方の影響で部材を回転させて部材ＹとＺを入れ替えた場合にモーメント線図が反転して出てしまいます。 モーメントの正負は実用上あまり問題にならないと思いますがＹとＺのモーメント線図を表示したときに違和感が出てしまうことがあります。
また建築系など業界によってはモーメントの正負が機械学会と反対になっていたりするので、 そのような場合はイメージ表示条件設定においてＹとＺそれぞれについてモーメントの反転や線図のみ反転ができるようになっていますのでそれで調整してください。 なおせん断力は部材座標の基準軸方向を＋としていますので、部材座標に対するせん断力の方向により正負の値が発生し、軸力は＋が圧縮、－が引張りになります。

はりの計算では荷重パターン条件で重力加速度に１（Ｇ）を入力すると部材の自重の影響を考慮することができます。自重を考慮したくない場合は重力加速度を０にします。

フレーム構造－平面・立体で自重を考慮する場合も荷重パターン条件の加速度条件で設定しますが加速度の方向は全体座標が基準となり、 通常は全体座標のＺ軸を上方向として構造を設定する場合が多いので、その場合はＺ軸が上に＋なので通常の自重を考慮する場合はＧｚに－１（重力が下向きなのでマイナスが付く）を入れます。 はりの計算とは符号が異なるので注意してください。自重を考慮したくない場合はＧｚを０にします。

なお従来あった“部材の自重を考慮”のチェックは廃止されており現在は荷重パターン条件のみの設定となります。

フレーム構造解析は有限要素法という計算方法で計算していますが、分布荷重は有限要素法で直接扱わずに要素を自動分割して内部的に節点を発生させ分布荷重を振り分けて集中荷重として計算する方法を使っています。 計算精度は一つの要素をいくつに分割するかの設定になります。

前述のように分布荷重（自重や加速度による荷重も同じ）は集中荷重に振り分けて計算するため誤差が発生しますが、 一般的には４分割して振り分けることで数％の誤差に収まるとされています。また計算結果も節点毎に求められるので内部節点が多いと一つの要素の変形やモーメント線図が滑らかに表示できるようになります。

計算精度は計算条件・単位設定で選択しますが標準の場合は４分割で精度係数として分割数が表示されます。 計算精度は最低（精度係数＝１）から高（精度係数＝８）、さらに任意では精度係数を自由に入力することができ、 計算精度を上げて分割数を多くすれば一つの要素の変形が滑らかに求められたり分布荷重がかかる場合の誤差を減らすことができます。 その代わり計算時の要素数や節点数が増えるので計算時間がかかるようになります。
 この内部節点についての計算結果は個別要素詳細では節点番号に［ ］が付いて表示されるようになっています。 また［モーメント・応力・座屈］タブにある“詳細表示”をチェックしても内部節点に関する計算結果が表示できるようになっています。

なお最大変位の発生場所も内部節点を含めた節点の計算結果の中から抽出されますので理論的な最大変位の発生場所とは誤差が出ることがあります。 この場合も計算精度を上げていけば発生場所の精度も向上しますが、計算精度を上げるのではなく発生場所近くにいくつか節点を設けて注目部分のみ実質的に精度を上げてやるのも一つの方法になります。

支持とはその構造物が外部（基礎等）からどのように支持されているかという意味になり、要素の接合方法とは全く異なります。 構造要素は節点を介して要素をつないでいくと剛接合でつながっていきます。
したがって要素をつないでいる節点の支持の種類がすべて「自由」であっても構造物としては剛構造となります。 ただし支持の設定がないと空間上に浮いた状態となり、僅かな荷重で無限に移動してしまうことになり計算ができません。 そのためその構造物を外部から支えている節点のみに支持を設定します。一般的な構造物であればアンカーに相当する節点に全固定かピン支持、他の節点は外部からの支持がなければ「自由」にしておきます。

節点の自由度はＸＹＺ軸方向の変位と、同じくＸＹＺ軸周りの回転で合計６自由度あり、その全てを固定したものが全固定となり、 変位のみ固定して回転は自由のものがピン支持となります。 その他、これら６自由度のどれを固定してどれを自由とするかでいろいろな支持の種類がありますが、あくまでも構造物を外部から支えるための支持ということを理解しておいてください。

なお支持の種類でバネ支持や柱脚、＊±自由などちょっと特殊なものもありますがこれらはマニュアルやチュートリアルを参照してください。

フレーム構造解析で言うところのトラス構造とは全ての節点がピン接合のものになり、三角形を基本とした構造物で軸力のみで構造をささえるものになります。 一見するとトラス構造にみえるものでも通しで鋼材が入っていたり斜材が溶接等で接合されていればラーメン構造となります。 この辺のところはフレーム１１－平面のチュートリアル“トラス構造とラーメン構造について”を参照していただいてフレーム構造解析でのトラス構造とラーメン構造の違いを理解しておく必要があります。

ラーメン構造においても補強のための斜材等を両端ピン接合としたトラス要素にしたい場合があり、 そのためにはその斜材の材料・断面性能の設定でトラス部材として設定しておくとその材料を適用した要素は自動的に両端がピン接合のトラス要素にすることができます。 ただしトラス要素は両端がピン接合なのでモーメントは受けませんが圧縮力は受けることができます。 補強用の斜材等でよく使われる細長い丸棒などは圧縮力を受けることが期待できないので、その場合は材料・断面性能の設定でブレース材として設定しておきます。

ブレース材も基本は両端がピン接合のトラス要素になりますが計算を実行してブレース材に圧縮力がかかっている場合はそのブレース材を無効にして再度計算し、 これを複数回繰り返して圧縮力を受けるブレース材が出ないようにする機能になります。ただしブレース材を使うと前述のように複数回計算を実行するので計算時間がかかりますので注意してください。

接合設定を使うと一端がピン接合、他端が剛接合の要素も設定でき、また両端をピン接合にしてトラス要素と同じにすることもできますが、 接合設定は１ヶ所当たり６節点１２要素を使って実現している機能ですので、単にトラス要素として設定したい場合は接合設定ではなく材料・断面性能でトラス部材として設定してください。
また材料・断面性能で“全てトラス部材”がチェック（凹んだ状態）されていると個々の材料の設定に関係なく全ての部材がトラス部材として計算されます。 最初に説明したようにトラス部材は両端がピン支持扱いとなるので三角形で構成されていない構造ではグラグラで不安定な構造になりＦＥＭ計算エラーが出るので注意が必要です。

構造要素の基本的な設定方法は節点を介してつなげていくのですが、つなぐべき節点を飛ばすなどのつなぎ方のミスで、 イメージ上は要素上に節点があり、つながっているように見えるものですが計算上はその要素とは関係なく空間上に節点が浮いている状態になっている場合があります。 それを浮き節点と呼び、またイメージ上でも他の要素と関係のない節点を孤立節点いいます。

浮き節点や孤立節点があると正常な構造にはならないのでＦＥＭ計算エラーが発生することが多く、 計算が通っても異常な計算結果となってしまうので注意が必要です。 この浮き節点や孤立節点があるかどうかは構造要素タブにある［浮き節点・孤立節点チェック］ボタンを押すことでチェックでき浮き節点や孤立節点が見つかった場合はメッセージに表示されます。 さらに“浮き節点自動修正”をチェックしてからこのボタンを押すと自動でつなぎ直すことができますが意図した構造になっているかはチェックが必要です。

ＦＥＭ計算エラーは通常は異常な変位が発生したときに表示され、異常な変位を起こしている節点番号が表示されます。 これは材料の強度不足や荷重が過大な場合に発生するので、例えば分布荷重はデフォルトではＮ／ｍｍのミリ当たりの荷重値を設定しますが、 これを総荷重と間違ったりした値を入力すると過大な荷重となりこのエラーが発生します。
また荷重が過大な場合以外にも前述のようにトラス部材の設定ミスで構造がグラグラになっている、浮き節点や孤立節点がある、 また支持の種類が適切でない場合でも発生することがあります。例えば門形ラーメンをピン支持で設定した場合に奥行き方向に荷重をかけると門が倒れてしまうようになりこのエラーが発生します。

ＦＥＭ計算エラーが発生した場合は次の順でチェックしてみてください。
１）過大な荷重がかかっていないか、材料の強度が弱すぎないか。
２）浮き節点や孤立節点がないか。
３）トラス部材を使っているときはトラス部材をやめてみたらどうか。
４）接合節点を使っている場合はピン接合を剛接合に変えてみたらどうか。
５）支持の種類でピン支持や全固定以外のものを使っている場合は支持の種類を全固定としてみたらどうか。

３～５でエラーが出なくなればその設定に関係した部分の構造に問題がありますのでその部分の構造を見直してください。 見直すポイントは元の構造がグラグラな不安定な構造となっていないかどうかになります。 天秤のような荷重によってバランスが取れるような構造では条件によっては計算が通ってしまうこともありますが天秤も基本的にグラグラな構造なので正常な計算にはなりませんので注意してください。
またちょっとした計算条件の変更でエラーが出たり計算が通ったりする場合の多くは構造に不安定な部分がありエラーが出るのが正常な動作であり、 計算が通る方が異常な場合もありますので、そういった意識を持って構造を見直してみてください。

断面係数Ｚは次に示すように慣性モーメントＩを断面の中立軸（伸びも縮もしない位置、重心図心を通る）から断面の端までの距離ｅで割ったものになります。

Ｚ＝Ｉ／ｅ

断面形状が図心を通るＸ軸、Ｙ軸について上下、左右が対称の場合にはｅはそれぞれの軸に対して同じ値になり断面係数は一つだけになりますが、 非対称の場合にはｅは長短二つになり断面係数も二つ求められます。そこで非対称の形状の断面性能については小さい方をＺｙＢ、ＺｚＢ、大きい方をＺｙＢ’、ＺｚＢ’とダッシュをつけて両方表示しています。 なお断面性能計算の項目名につく座標系はフレーム構造解析の部材座標系となっており“Ｂ”がついて表示されますが、 印刷設定で“項目名をＪＩＳに準拠したものとする”をチェックすると項目名はＸＹ座標系となり“Ｂ”も外して出力できるようになります。

曲げ応力σは次に示すように曲げモーメントＭを断面係数Ｚで割って求められます。

σ＝Ｍ／Ｚ

したがって通常は応力が高くなる不利な条件（安全サイド）として応力が大きくなるように断面係数の小さい方を強度計算に使用します。 また断面性能計算から構造解析の材料登録ができますがこのときは断面係数の小さい方のみが登録されるようになっています。

今まで正常に計算できたり印刷ができていたのに、ある日突然エラーが出て起動できなくなったり印刷ができなくなったりすることがあります。 このエラーはコマンド終了時にダイアログの位置や大きさ、各種設定内容を保存して次回起動時に終了時の状態を再現するための起動時デフォルトデータが壊れたときに発生します。

対策としてはコマンド選択メニューにある［データファイル管理］を起動して起動時デフォルトデータのリストボックスでエラーの出ているコマンド名を選択して右にある［初期化］ボタンをクリックして初期化してください。 これを初期化するとインストール直後に近い状態となりますので各種設定等を変更している場合は再度設定してください。 また起動時デフォルトデータは後から作られるデータファイルなのでアンインストールしても削除されず、そのまま再インストールしてもエラーが直らない場合があります。 再インストールする場合はマニュアルの「アンインストール後の処理」を参照してインストールフォルダと作業フォルダを削除してから再インストールしてください。

フレーム構造解析の計算方法は有限要素法になります。

現在では、温度分布、電場、磁場、音場、流体、気象などのさまざまな現象の解析に用いられている有限要素法で対応ソフトウェアも様々なものが開発されています。 一般的な有限要素法は平面であれば三角形や四角形、立体であれば四面体や六面体などの要素を使っていますが、 フレーム構造解析では２節点骨組要素を使った有限要素法になっています。 すなわち２つの節点を結んだ構造要素が有限要素法での一つの骨組要素（フレーム要素）ということになります。

前述のようにフレーム構造解析の計算方法は有限要素法を使っており、比較的簡単な構造でも膨大な計算量になりますので、 有限要素法の計算の流れを追って手計算で検算することは事実上不可能です。 ただしフレーム構造解析のような解析ソフトは計算結果が信頼できないと安心して使うことができませんので何らかの方法で検証したいというは技術者としては当然のことです。

そこで良く使われる検証方法として手計算で厳密解（近似値ではなく正確な答え）を求められる比較的単純なモデルを使って手計算の厳密解と解析ソフトの計算結果を比較します。 有限要素法を使った解析ソフトは単純なモデルから複雑なモデルまで同じ計算方法を使うので、 手計算と比較できる単純なモデルで計算精度が検証できれば複雑なモデルの場合でもそれなりの精度で計算できていると推定できます。

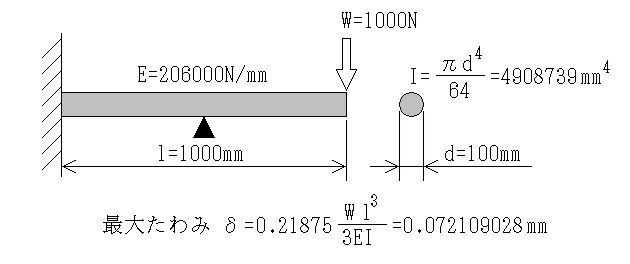
検証の事例として次のような片持ちはりで手計算とフレーム構造解析でどうなるか試してみましょう。

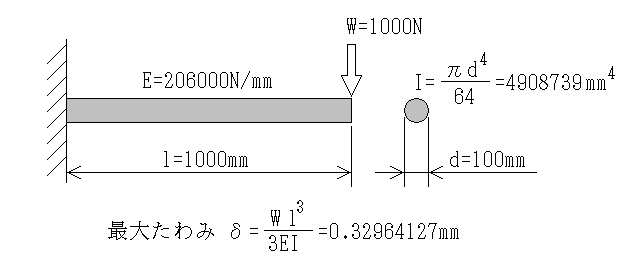
これと同じモデルをフレーム構造解析１１の立体で設定して計算してみます。 ただし自重の影響は受けないように加速度は全て０とし有効数字も８桁、断面性能の有効数字は上記のＩに合わせて７ケタにしておきます。

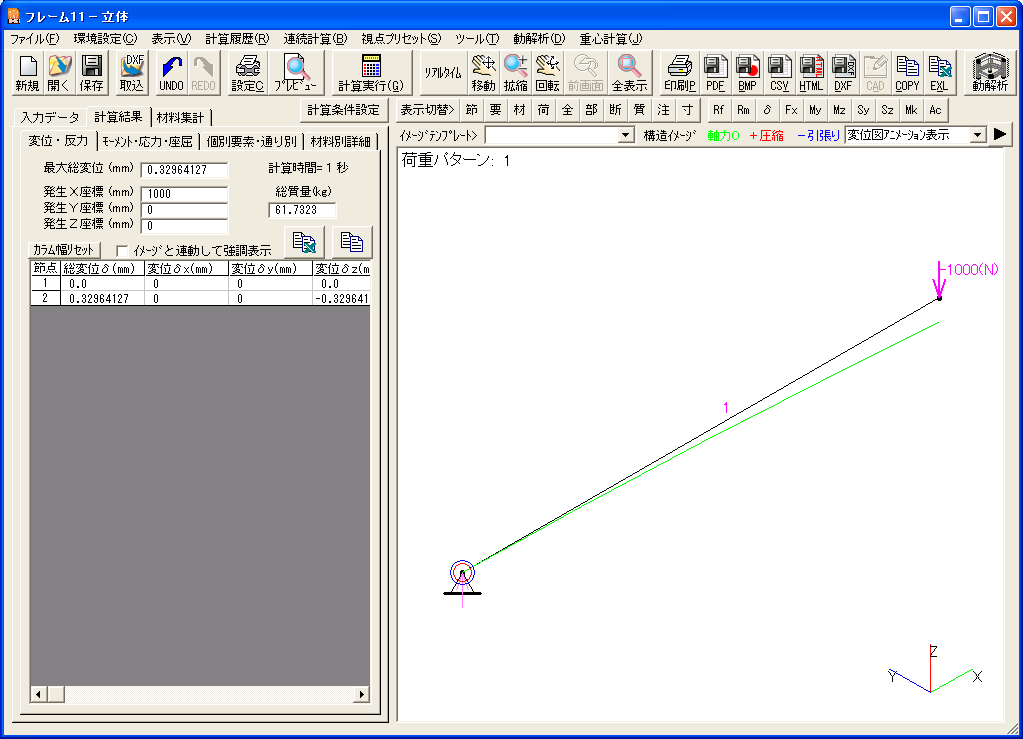
最大総変位（最大たわみ）は手計算と全く同じ値が得られています。

次に中間に節点を挿入して要素数を増やしてみたものを示します。 要素番号もバラバラになるようにつなぎ直しています。こうすることで有限要素法の計算量も増え計算する順番も異なってくるので何か計算上の問題があれば計算結果が違ってくるはずです。

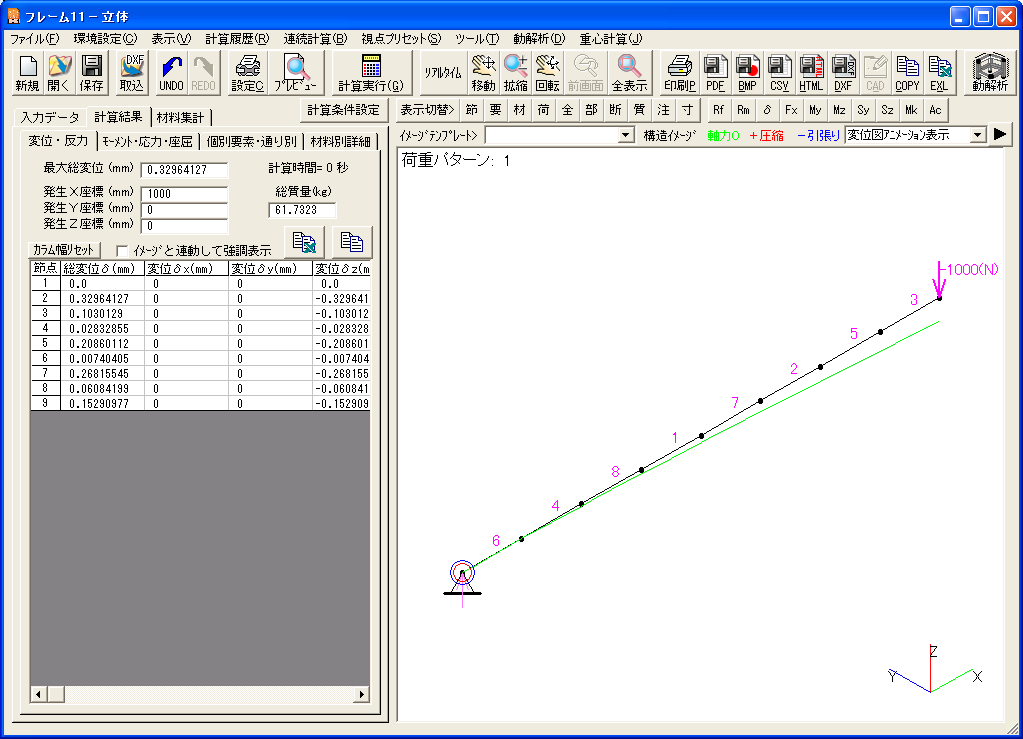
節点を増やし要素を適当につなぎなおしても最大総変位の値は全く変わりませんので節点数や要素数の影響を受けないことも分かります。 このまま中央の節点にピン支持の設定をして不静定はりの一つの一端固定中央支持はりにして計算してみます。

最大総変位は０．０７２１０９０３ｍｍとなっています。では手計算で厳密解を求めてみましょう。

有効数字７桁と考えればこちらも手計算と同じ値と言えるでしょう。 また有限要素法では静定、不静定などを意識することなく簡単に条件を変えて計算できることが分かります。 なおこの手計算の式の誘導は別途、材料力学の参考書等で調べてみてください

このように手計算で厳密解が求められるモデルを使って検証するか、あるいは他の実績のある有限要素法のソフトウェアと同じモデルで比較するのが有限要素法の解析ソフトの検証方法となります。 ただしフレーム構造解析のユーザー数は既に２０００ユーザーを超えており実績のあるソフトウェアになりつつあると考えられます。 なお門形ラーメン等で剛比を使った手計算用の計算式がありますがこれは近似式になり、 近似式で検証してもどちらの誤差なのか分かりませんので手計算による検証にはあくまでも厳密解が求められるモデルで比較してみてください。

フレーム構造解析は機械設計用にスタートした汎用の解析ソフトになり、 建築・土木関係の要望を多く取り入れて改良してきましたが特定の業界の法令に準拠したようなものではなく、公的機関の認定を受けているものでもありません。

ただしユーザーの中にはフレーム構造解析を使った計算書で審査機関に確認申請を行ったり、 役所に提出したりしています。 これらの計算書の作成は各ユーザーが工夫されて作られているものでひな形のようなものは提供しておりませんが、 計算書の提出先から「どのような計算方法を使っているのか」とか「検算はできるのか」などが聞かれるようなので回答にあたってはＡ１９やＡ２０、次のＡ２２などを参考にされると良いと思います。

フレーム構造解析で使っている有限要素法の解析エンジンは算生会、黒田英夫氏作成の３次元ラーメン構造解析プログラムの解析エンジン部を正式にライセンスを受けて組み込んでいます。 このプログラムの取扱説明書（3Dﾗｰﾒﾝ構造F説明.pdf ）には有限要素法の基礎的な計算式が解説されておりますので同氏の許可を得て該当部分を転載したものを次に示します。

以上、算生会、黒田英夫氏作成の３次元ラーメン構造解析の取扱説明書（3Dﾗｰﾒﾝ構造F説明.pdf ）より、有限要素法についての解説部分を同氏の許可を得て転載いたしました。

フレーム構造解析ではこの有限要素法を使った解析エンジンで各節点の変位や各要素の軸力、せん断力、モーメントを求めてから、各種の応力や安全率を計算しています。

先の解説の中で線分要素の物性として“Ｋ：サンブナンの捩り定数”が出てきています。 これはねじりに関する剛性を表した定数でフレーム構造解析の有効断面２次極モーメントのことになります。

円断面ではサンブナンの捩り定数は断面２次極モーメントと一致しますが円断面以外はねじりを受ける面が減ってくるので断面２次極モーメントとは一致せず、そのためフレーム構造解析では“有効”の文字をつけて表しています。 またねじりモーメントからねじり応力を求める極断面係数も同様の理由で“有効”の文字をつけて有効極断面係数としています。 マニュアルにはいつくかの決まった形状での有効断面２次極モーメントと有効極断面係数の計算式を載せていますがこれらに当てはまらない形状では手計算では求められません。

フレーム構造解析の「断面性能計算」では前出の算生会、黒田英夫氏が作成した２次元平面の有限要素法を使った捩り解析エンジンで任意の形状の有効断面２次極モーメントが求められるようになっており、 ねじりモーメントによるせん断応力の解析を行うので有効極断面係数も求められるようになっています。 求めた有効断面２次極モーメントや有効極断面係数を含む断面性能は共通のフォルダに登録してフレーム構造解析の他のコマンドで使えるようになっています。

この２次元平面の有限要素法を使って捩り解析を行い有効断面２次極モーメント（サンブナンの捩り定数）や有効極断面係数を求められる機能は他に類を見たことがありません。 他の類似の解析ソフトではサンブナンの捩り定数は決まった形状以外は対応できないとか、ねじりの影響は少ないので０にしておくとかの対応を見たことがありますが、 ＣＡＤＴＯＯＬフレーム構造解析はここまできっちり対応ができていることが分かっていただけたのではないでしょうか。